- Source of uncertainiy
1. Inherent stochasticity in the system bening modeled
2. Imcomplete observability
3. Incomplete modeling (model that must discard some of the information we have observed)
- Frequentist probability :related directly to the rates at which events occur
- Bayesian probability : related to qualitative levels of certainty (degree of belief)
- Probability mass function (PMF) : Probability distribution over discrete variables, denote as P
x 변수일 확률 : x ~ P(x) , P(x=x)
- Joint probability distrubition : many variables at simulataneously, P(x=x, y=x)
- Probability density function (PDF) : Continuous variables and probability density function, p(x)
- Marginal Probability : Probability distribution over the subset
- Conditional Probabiltiy :
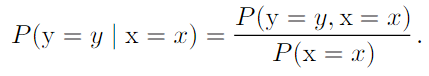
.Chain rule of conditional probabilities
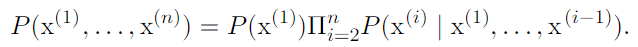
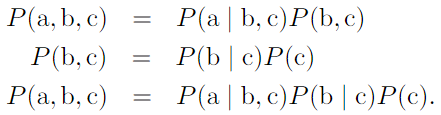
- Independence : notation, x⊥y
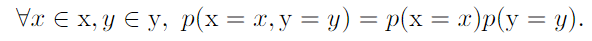
- Conditional independent : notation, x⊥y | z (z : given random variable)
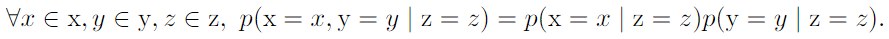
- Expectation, Expected value :
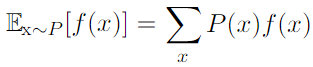
- variance, standard deviation (square root of the variance) :
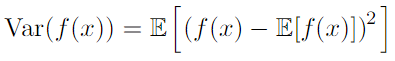
- Covariance : How much two values are linearly related to each other
.independent two variable have zero convariance
* independent exclude nonlinear relationship (depedent and zero covariance is possible)
Correlation : normalize the contribution of each variable
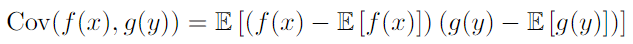
- Bernoulli Distribution: single binary random variable, parameterized, φ ∈[0,1]
- Multinoulli (Categorical) Distribution: single discrete variable with k different states (k is finite),
- Gaussian Distribution (normal distribution):
*precision : square and inverse variance

.The reason why normal distribution is a good default choice
1. many independent random variables is approximately normally distributed
2.out of all possible probability distributions with the same variance,


- Exponential and Laplace distribution : sharp peak probability mass at arbitary point u
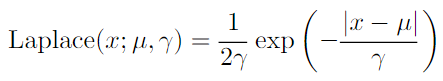
- Dirac distribution and empirical distribution: zero valued everywhere except 0 but integrates to 1
Dirac delta distribution is used as empirical distribution
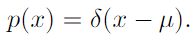
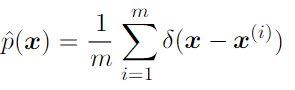
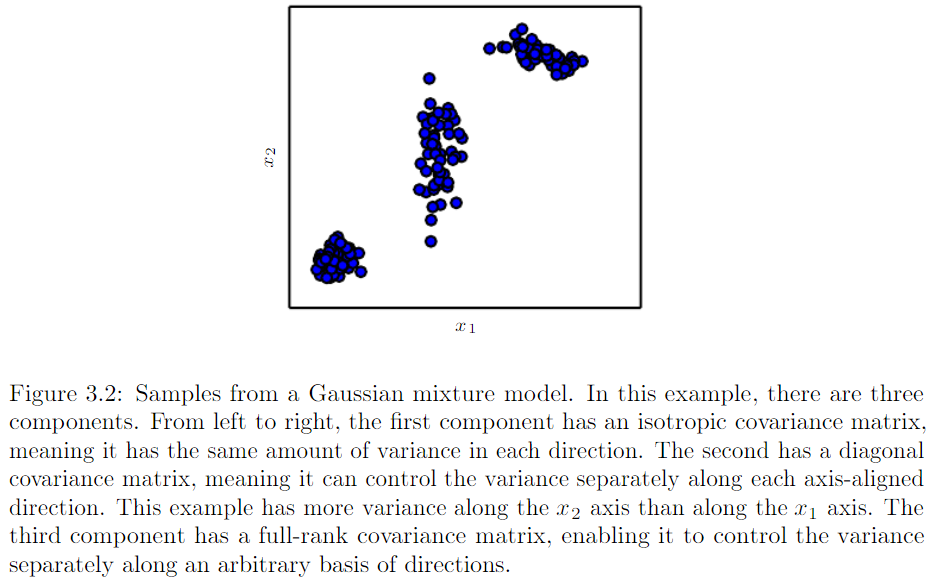
- Mixtures of distributions: A mixture distribution is made up of several component distributions
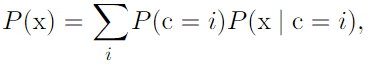
Gaussian mixture model :
.p(x|c=i) are Gaussians
.each components has a separately parametrized mean and covariance
.universal approximator : any smooth density can be approximated with any specific nonzero amount of error by a Gaussian mixture model with enough components
.parameter of gaussain mixture(mean,covariance) specify the prior probability P(c=i)
prior probability: P(c), model's beliefs about c before it has observed by x
posterior probability : P(c|x), computed after observation of x
- logistic sigmoid :
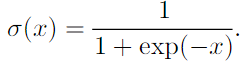
- Bayes' rule: P(x|y) 를 알고 싶을 때, P(y|x) 와 P(x) 를 알면 구할 수 있음
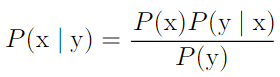
- Information Theory :
Basic Intuition
1. 자주 발생하는 사건 정보가 거의 없다. (ex: 내일은 해가 뜬다)
2. 잘 발생하지 않는 사건은 정보가 많다. (ex: 내일 해가 뜰 때 태양풍이 일어난다)
3. 독립적인 사건은 추가적인 정보를 가진다.
- Shannon entroy: 특정 분포에서의 정보(불확실성)의 양의 총 합. 분포를 encoding 하는데 필요한 최소의한 bits 수
.분포가 deterministic 할 수록 entropy 가 낮음, 분포가 Unifrom 할 수록 entropy 가 높음
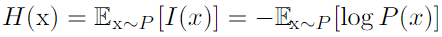
- Kullback-Leibler (KL) divergence: 같은 random variable x 에 대한 두 개의 분포 P(x), Q(x) 의 다른 정도를 계산
.Asymmetry 함
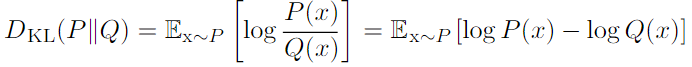
.Cross entory : Q에 대한 Cross entory 의 최소화는 KL divergence 의 최소화와 같음
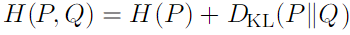
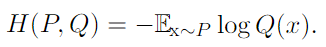
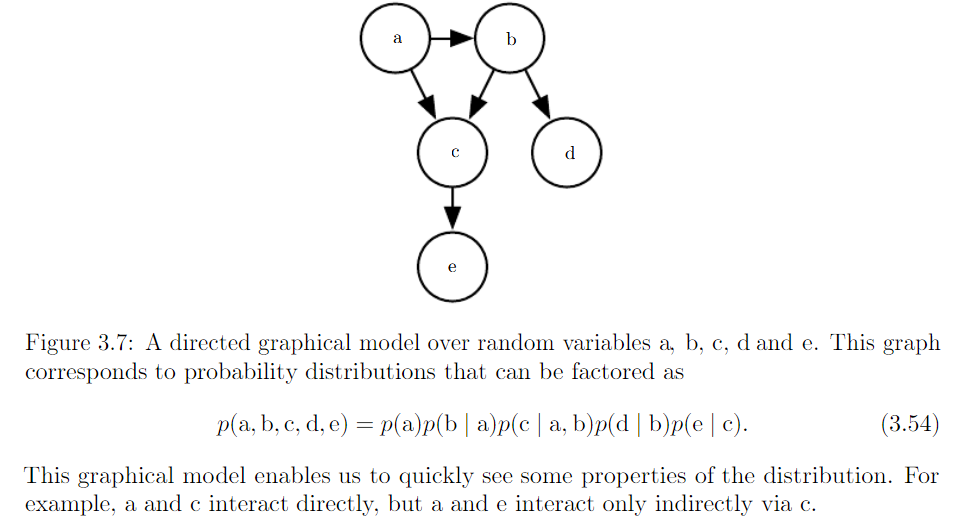
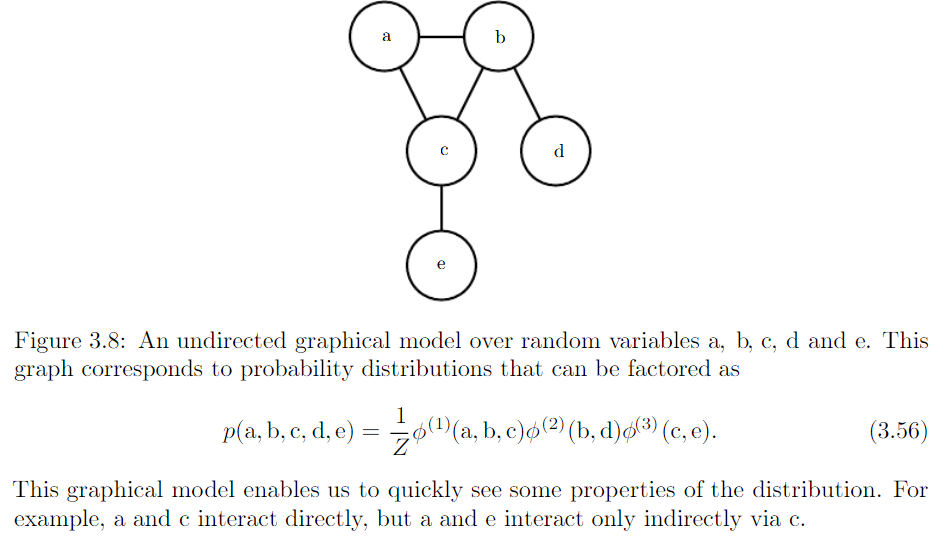
- Structured probabilistic models (graphical model) : factorization of a probability distribution with a graph
*factorization probability distribution : greatly reduce the number of parameters needed to describe distribution
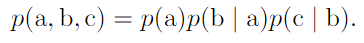
*graph : a set of vertices that be connected to each other with edge
'ML, DL > Deep learning text book' 카테고리의 다른 글
| 4. Numerical Computation (0) | 2022.09.04 |
|---|---|
| 2. Linear Algebra (0) | 2022.09.03 |